Una paradoja es una situación que desafía el sentido común y da como resultado una situación imposible. Aquí tienes 13 paradojas.
¡Ojo! Hago directos en Twitch sobre desarrollo web, ¿Te apuntas? ManzDev
13 paradojas que quizás no conocías
Escrito por J. Román Hernández Martín
Por norma general, ante muchas situaciones, acostumbramos dejarnos llevar por el sentido común y la lógica, que son las mismas que nos dictan los parámetros para pensar y decidir en base a un determinado escenario.
Sin embargo, en ciertas ocasiones, las cosas terminan siendo muy diferentes a lo que pensabamos en un principio, o directamente, desafían el sentido común y la lógica, llegando al punto de resultar imposibles. A este concepto se le denomina paradoja.
Veamos un listado de 13 paradojas muy curiosas e interesantes, algunas de ellas bastante conocidas:
1. El gato de Schrödinger

Una de mis paradojas preferidas es la del experimento teórico de El gato de Schrödinger. Pertenece al campo de la física, más concretamente al de la física cuántica.
En el experimento de Schrödinger, tenemos una caja totalmente opaca, con 3 elementos en su interior: un gato (vivo), una botella con un gas venenoso y un aparato con una partícula radioactiva, la cual tiene una probabilidad del 50% de desintegrarse.
En el caso de desintegrarse, la botella libera el gas, matando al gato. En el caso de no desintegrarse, no ocurre absolutamente nada (y el gato vive).
La paradoja consiste en que, según nuestro sentido común, el gato estará vivo o muerto pero no podremos saberlo hasta abrir la caja. Según las leyes de la física cuántica, el gato está vivo y muerto (los dos estados a la vez) hasta que se abra la caja y se compruebe.
En el mundo de Internet es muy conocida (quizás por el mero hecho de existir un gato en la demostración) y ha llegado hasta el punto de tener su propio Schrödinger Nyan cat [*].
Existe una variación del gato de Schrödinger, denominado El suicidio cuántico, aunque también podríamos denominarlo la venganza del gato de Schrödinger, ya que se desarrolla la teoría desde el punto de vista del gato (y con un humano).
Youtube | El gato de Schrödinger
Más información | Cat Paradox Paper
2. El cuadrado perdido
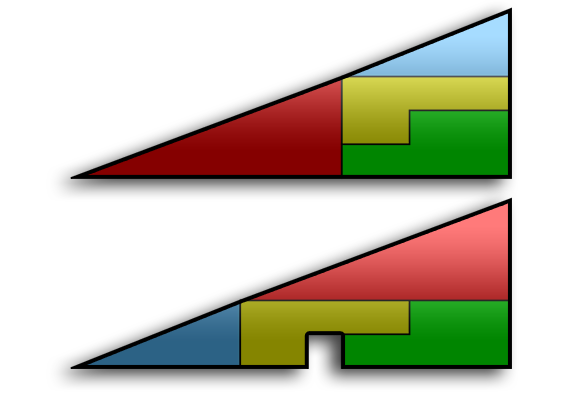
El problema del cuadrado perdido es una paradoja muy conocida y utilizada en el inicio del estudio de la geometría, dentro del campo de las matemáticas.
La paradoja consiste en la reordenación de los elementos del triángulo de la imagen superior. ¿Cómo es posible que sólo reordenando las mismas piezas, nos sobre ese espacio cuadrado?
Obviamente, tiene truco y se trata sólo de una ilusión óptica. En los siguientes enlaces se puede observar claramente la explicación de ese cuadrado que desaparece.
Animación visual | El cuadrado perdido
Solución visual | Solution to Missing Square
3. La cinta de Möbius
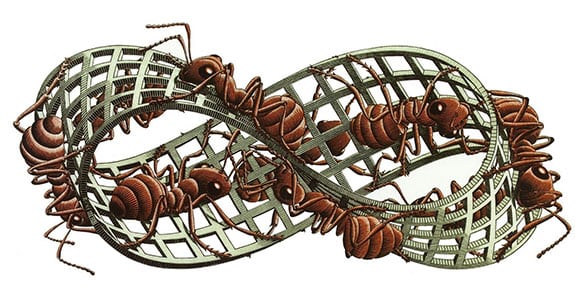
La banda o cinta de Möbius (o Moebius) es una figura simple y muy sencilla de construir que se utiliza mucho en el ámbito de las matemáticas (geometría) o en topología.
Entre las propiedades de esta cinta, que son las que la hacen paradójica, quizás la que más destaca es que tiene una sola cara y un solo borde, lo que lo convierte en algo similar a un objeto imposible (pero obviamente, posible), al puro estilo de M. C. Escher, de hecho, la imagen superior es de su autoría.
Youtube | Construir una banda de Möbius
Más información | La banda de Möbius
4. La paradoja del abuelo

La paradoja del abuelo es una paradoja física muy utilizada en la ciencia ficción, ya que tiene su base en los viajes en el tiempo. Es muy conocida y se ha utilizado en muchas obras, como por ejemplo Terminator, Regreso al futuro o Futurama.
Suponiendo el caso de que una persona pudiera viajar hacia atrás en el tiempo, retrocediera varios años y matase a su abuelo antes de que tuviera descendencia (concretamente al padre del viajero del tiempo), este no habría nacido ni hubiera tenido hijos, por lo cual el viajero del tiempo tampoco nacería ni le sería posible viajar en el tiempo para matar a su abuelo.
Es curioso como se han ideado ciertas soluciones a esta paradoja para hacer posible el suceso, como la existencia de universos paralelos, líneas temporales alternativas o tantas otras. Otra paradoja relacionada con la ciencia ficción, es la paradoja de Fermi.
Autor de la paradoja | Le voyageur imprudent, René Barjavel
5. ¿El huevo o la gallina?

Probablemente, la paradoja más conocida del mundo.
«¿Qué ocurrió primero, la gallina o el huevo?». En el caso de ser la gallina, se plantea que la gallina tuvo que salir de un huevo. En el caso de ser el huevo, éste lo tuvo que poner una gallina.
Este dilema, adjudicado a las ramas de la filosofía, es muy conocido en la cultura popular y se han realizado multitud de teorías sobre ella. Por ejemplo, Aristóteles afirmaba que lo primero en existir fue la gallina, mientras que Stephen Hawking asegura que lo fue el huevo.
6. La paradoja del cumpleaños
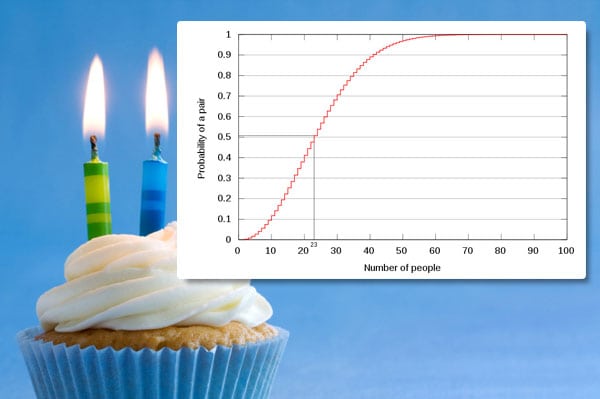
Esta paradoja, pertenece al campo de las matemáticas, más específicamente a la estadística.
Se dice que en un cumpleaños con 23 personas, existe una probabilidad de más del 50% de que al menos dos personas cumplan años el mismo día. De hecho, si hay 50 personas, la probabilidad es casi del 100% (97% exactamente).
Esta paradoja sorprende mucho por una especie de ilusión mental, ya que el sentido común dicta lo contrario que la demostración matemática. Aún así, si no te crees la paradoja, puedes comprobarlo en el simulador visual del enlace.
Applet | Simulador de la paradoja del cumpleaños
Más información | Birthday Problem
7. El teorema de los infinitos monos

Otro teorema clásico y popular, que quizás no llega a ser paradoja, pero sí merece la pena añadir en este listado, es el teorema de los infinitos monos. Es tan conocido que ha sido referenciado en multitud de obras, desde el libro La guia del autoestopista galactico, de Douglas Adams, hasta en varios capítulos de Los Simpsons, entre muchos otros.
El teorema afirma que si un número infinito de monos escribieran a máquina por un intervalo infinito de tiempo, acabarían escribiendo las obras de Shakespeare.
Aunque el teorema original versaba sobre un sólo mono y cualquier libro de la Biblioteca Nacional Francesa, la cultura popular hizo que se popularizara esta versión. Hace varios años, también se llevó a cabo un experimento (Experimento Vivaria) donde tomaron fotos y realizaron pruebas a varios monos, para ver que eran capaces de escribir y durante cuanto tiempo.
Más información | Infinite monkey theory
Experimento | Informe del experimento Vivaria
8. La paradoja de Monty Hall

Otra paradoja perteneciente al campo de la estadística es la paradoja de Monty Hall, también llamada la paradoja de las tres puertas.
En un concurso televisivo tenemos tres puertas cerradas. Detrás de una de ellas hay un coche, mientras que detrás de las otras dos, hay una cabra respectivamente.
Después de que el concursante haga su elección (y antes de comprobar si ha acertado), el presentador abre una de las puertas no elegidas donde sabe que hay una cabra y le pregunta al concursante «¿Está seguro de querer abrir esa puerta o quiere elegir otra?»
El sentido común dicta que no hay diferencia entre cambiar o no la elección de la puerta, sin embargo, el problema tiene trampa, ya que si nos quedamos con la puerta elegida inicialmente tenemos menos probabilidades de acierto que si cambiamos de puerta.
Simulador | Monty Hall Simulator
Más información | La paradoja de Monty Hall
9. La paradoja de Abilene

La paradoja de Abilene es una situación estudiada en el campo de la sociología en la que un grupo de personas realizan una acción que no quieren realizar (individualmente) porque ningún miembro está dispuesto a objetar algo o negarse.
En una calurosa tarde, un matrimonio y su suegra están jugando al dominó a la sombra. El suegro propone hacer un viaje a Abilene (un caluroso viaje de más de 80km). La mujer acepta «¡Gran idea!». El marido dice «A mi me parece bien, espero que a tu madre también». «Por supuesto», responde.
Tras realizar el viaje, con más horas de lo previsto, malhumorados y agotados, la suegra dice «Menudo viaje. Hubiera preferido quedarme en casa, pero acepté porque estaban muy ilusionados». El marido reconoce que vino sólo para satisfacer al resto ya que pensó que estarían aburridos, mientras que la mujer sostiene que aceptó para no estropear el plan de los demás.
Finalmente, quedan perplejos. Decidieron en común hacer un viaje que ninguno de ellos quería hacer.
Otros experimentos sociológicos similares, en los que puedes tomar parte, podrían ser La mujer y el puente o La princesa y el toro.
10. La paradoja de los gemelos

La paradoja de los gemelos (o de los relojes) es un experimento teórico catalogado dentro de la física (relatividad).
Dos gemelos deciden realizar un experimento: Uno de ellos viajará en una nave a la velocidad de la luz a una estrella, mientras que el otro se queda en la Tierra.
De acuerdo con la dilatación del tiempo (teoría de la relatividad), cuando el gemelo viajero vuelva a la Tierra, será más joven que el que se quedó, ya que el tiempo del gemelo de la nave va más despacio que el de la Tierra.
Youtube | Paradoja de los gemelos
Más información | Twin Paradox
11. El dilema del prisionero

El dilema del prisionero no es una paradoja en sí, pero es un problema dentro de la rama de la teoría de juegos que puede considerarse paradójico.
La policía arresta a dos sospechosos. No hay pruebas suficientes para condenarlos, sin embargo, se les separa en dos celdas diferentes y se les ofrece el mismo trato: Si uno de ellos confiesa y su cómplice no, se condenará 10 años al cómplice y se liberará al delator. Si ambos confiesan, se condenarán a 6 años cada uno. Si ninguno confiesa, sólo podrán encerrarlos durante 6 meses por cargos menores.
El experimento muestra que dos personas no cooperarán, incluso aunque en ello vaya el interés de las dos.
Es curioso saber que, en una variación de este problema, el prisionero iterado, se repite varias veces el mismo juego, añadiendo la posibilidad de castigar al otro jugador por la no cooperación en partidas previas. El incentivo para defraudar termina siendo superado por la amenaza del castigo, por lo que conduce a una cooperación forzada.
Más información | Dilema del prisionero
12. La paradoja del hotel infinito

El Hotel infinito de Hilbert es una metáfora paradójica relacionada con el mundo de las matemáticas.
Dos grandes empresarios con un hotel gigante, tienen el problema de que quieren garantizar a los clientes que siempre tendrán una habitación disponible para un nuevo cliente. Como el hotel actual, con 1.000.000 de habitaciones no era suficiente, tomaron cartas en el asunto.
Los dos empresarios decidieron construir el primer hotel con habitaciones infinitas. Un número infinito de habitaciones garantizaba dar alojamiento a un número infinito de clientes. Pero al llegar un nuevo cliente, se vieron de nuevo con el mismo problema.
Para ello idearon una solución. Dar alojamiento a los clientes con la única condición de que si llega un nuevo cliente, tienen que abandonar su habitación e irse a la habitación siguiente (+1). Así, el nuevo cliente se hospedaría en la habitación 1, y el resto se iría rodando a la habitación directamente siguiente. Como el hotel tiene un número infinito de habitaciones, no habría última habitación.
Más información | El Gran Hotel Cantor
Autor | David Hilbert
13. La paradoja de la serpiente

Finalmente, para terminar, otra paradoja popular, muy similar al de el huevo o la gallina, denominada La paradoja de la serpiente, muy utilizada en campos y materias de filosofía.
Un uróboro es una palabra griega que representa a un animal que engulle su propia cola, formando un círculo. Si dicho animal, por ejemplo, una serpiente, comienza a comerse su cola y termina tragándose todo su cuerpo... ¿Dónde estaría la serpiente?
La paradoja entra en juego cuando nos damos cuenta que la serpiente se encuentra dentro de su propio estómago, pero simultáneamente sigue comiéndose a sí misma.
Más información | Uróboro
