Multiplicación: Algoritmo de Booth

¡OJO! Si no eres informático o estudiante de ingenieria computacional, probablemente este artículo no te interese.

Hace unos días necesité implementar el algoritmo de Booth en C++ para una parte de una de las prácticas de la asignatura Teoría de autómatas y lenguajes formales y la verdad, aunque existe bastante información, eché en falta una explicación didáctica para comprender el procedimiento desde un punto de partida. Asi pues, en este artículo intentaré explicar el procedimiento del algoritmo lo mejor posible.

El algoritmo de Booth es un método rápido y sencillo para obtener el producto de dos números binarios con signo en notación complemento a dos.

Debemos saber que un número binario está formado por bits de ceros y unos, y que se puede traducir a decimal fácilmente de la siguiente forma:

Sabiendo que la posición de cada bit es 2^n (elevado a n) y partimos de n=0 de derecha a izquierda, sólo queda realizar la suma total de multiplicar por dicho bit, en este caso, lo que muestro a continuación:
0·2⁷+1·2⁶+0·2⁵+1·2⁴+0·2³+1·2²+1·2¹+0·2⁰ = 86.

También debemos saber que el complemento a uno de un número binario es cambiar sus ceros por unos, y sus unos por ceros (complementar): (010010 -> ca1: 101101) y que el complemento a dos de un número binario es el resultado de sumar 1 al complemento a uno de dicho número binario (NOTA: En el Ca1 sólo se complementa si el número es negativo):

Realizar una suma con dos números binarios es tarea fácil, pero la multiplicación resulta algo más complicada. Con el algoritmo de Booth, resulta mucho más sencillo de implementar. Partimos del ejemplo de la multiplicación 6·2=12:

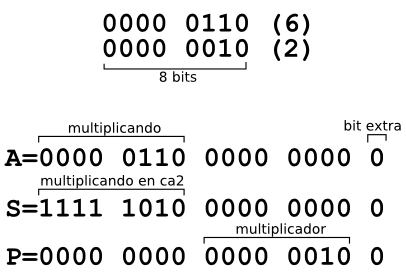
Como se puede ver en la imagen superior, partiendo de los números binarios de la multiplicación 6·2 (multiplicando y multiplicador) creamos tres nuevos números binarios del doble de tamaño (16 en el ejemplo): A, S y P.

Partiendo del número P (producto) comenzamos a comparar los últimos 2 bits de la derecha, siguiendo los casos base del recuadro:

Se realizará esta comparación 8 veces en este ejemplo (número de bits de los operandos) y al final de cada comparación, realizamos un desplazamiento de un bit hacia la derecha, manteniendo el último bit de la izquierda, y descartando el último bit del lado contrario. Si hacemos una traza paso a paso nos quedarían los siguientes resultados:

Finalmente obtenemos el número en binario resultante (12 en este ejemplo), descartando el bit extra que hemos añadido al principio del procedimiento y que se encuentra en el extremo a la derecha.

Espero que esto les sirva tanto como me sirvió a mi en su momento.