El método Simplex Revisado
El método Simplex es un algoritmo de George Dantzig para resolver problemas de optimización (de la rama de programación lineal).
En este artículo voy a realizar el proceso paso a paso y de forma sencilla, utilizando el método Simplex Revisado, una versión computacional reducida del algoritmo, que puede que a varios compañeros que cursen esta asignatura les venga bien.
Identificar el problema
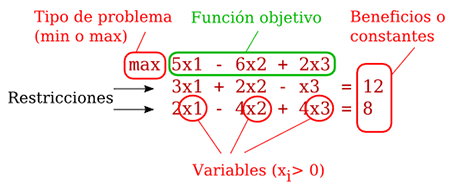
Es muy importante tener siempre presente con que tipo de problema estamos trabajando: mínimo o máximo (ya volveremos a esto más tarde), que las variables Xi con las que trabajamos son positivas, y que los beneficios no pueden ser negativos.
En este último caso, habría que cambiar de signo a toda la restricción implicada (con beneficio negativo).
Habría que contemplar además, el caso en el que las restricciones sean inecuaciones. Si así fuese, hay que tener presente el añadir la resta de una variable de excedente (inecuación mayor/igual) o añadir la suma de una variable de holgura (inecuación menor/igual), convirtiendo así las inecuaciones en ecuaciones.
Método de las dos fases
Partiendo de un ejemplo inicial (en rojo) vamos a realizar el llamado método de las dos fases.
Añadimos la suma de una variable artificial nueva por cada restricción (en este ejemplo X4 y X5) y reemplazamos la función objetivo por la minimización de la suma de todas las variables artificiales.
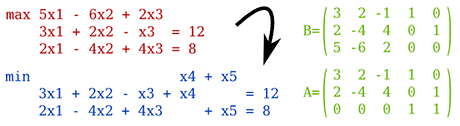
A su vez, y para cada una, crearemos una matriz A (la que empezaremos a usar) y una matriz B, que no es más que el valor de los coeficientes de las restricciones, sólo que la función objetivo, se desplaza a la última fila.
Debe notarse que en la matriz B también tiene los coeficientes de las variables artificiales (X4 y X5) en las restricciones.
Tabla inicial
Construiremos una tabla para ir resolviendo el problema, que constará de varias zonas:
- Columna VB: En la primera columna (Variables Básicas), colocaremos todas las variables artificiales añadidas (en este caso sólo 2: X4 y X5). En la última fila, colocamos -w que representa que estamos en la fase 1.
- B-1: La inversa de la base, que inicialmente no es más que la matriz identidad.
- Columna derecha: Quedará siempre una columna vacía, donde se deberá rellenar con ceros, salvo la posición que pertenece a la última fila, que colocaremos un 1.
- Constantes: Esta columna representa los beneficios asociados a la variable artificial de la restricción donde fue añadida.
Ahora vamos con las dos más peliagudas:
- -CBt · B-1: Esta zona se el resultado de la multiplicación entre la traspuesta de los coeficientes de la base, en negativo (a la izquierda, en azul) y la inversa de la base de la tabla actual (B-1).
- Vo: El valor objetivo de la tabla se calcula multiplicando las matrices correspondientes al punto anterior y a las constantes de las variables artificiales de la tabla actual.
Costos relativos
Cada vez que terminemos una iteración de la tabla (como ahora), deberemos calcular los costos relativos para saber si debemos continuar o ya tenemos una solución óptima.
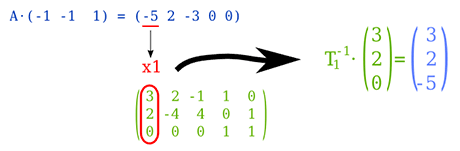
Para calcularlos, multiplicamos la matriz A por la última fila (-w) de la tabla. Esto nos da una matriz con los costos relativos que deben ser:
- Problema de mínimos: Los valores deben ser positivos (mayores o iguales a 0). Si son negativos, se optará por seleccionar el más negativo (regla de Bland).
- Problema de máximos: Los valores deben ser negativos (mayores o iguales a 0). Si son positivos, se optará por seleccionar el más alto. Nota: Este problema concreto es de máximos, pero notar que estamos en la fase 1, que se convirtió en un problema de mínimos. Al salir de la fase 1, volverá a ser un problema de máximos de nuevo.
Quizás lo ideal sería realizar la regla lexicográfica para evitar el ciclado, ya que es más eficiente y requiere menos iteraciones. Aún así, en este caso usaremos Bland, ya que se ve más claro.
Variable entrante
Cómo se ve en la imagen anterior, en nuestro ejemplo seleccionamos -5 (de los candidatos -5 y -3), correspondiente a X1, por lo que extraemos de la Matriz A, la columna perteneciente a X1.
Es ahora cuando debemos multiplicar la Tabla actual (T1-1) por esta columna extraída y nos dará la columna pivote (C.P.) a utilizar para obtener la segunda tabla (T2-1).
Variable saliente
Sabemos que la variable entrante es X1, sin embargo, no conocemos cuál es la saliente. Para esto, lo que se hace es dividir los beneficios entre el número de la columna pivote y el valor más pequeño es el que saldrá de la base.
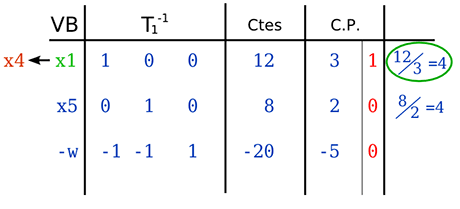
Calcular la siguiente tabla
Para conseguir la siguiente tabla, debemos convertir la columna pivote (C.P.) en la columna indicada en rojo, a su derecha.
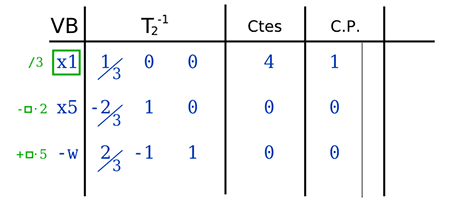
Entonces, procederemos como se hace en las eliminaciones por Gauss-Jordan. En nuestro ejemplo, la primera fila se divide entre 3, obteniéndose una fila pivote (no confundir con columna pivote) que utilizaremos para reducir las demás.
La segunda fila se calcularía como: la segunda fila de la tabla T1-1 menos la fila pivote por 2. Idem con la tercera. Volveríamos al paso del cálculo de costos relativos, a una nueva iteración.
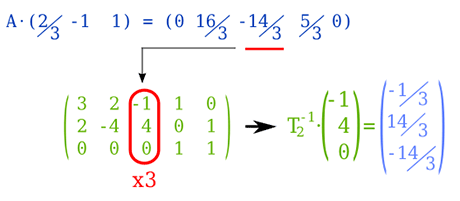
Seguiríamos actuando como hasta ahora, hasta que no podamos seleccionar variables entrantes (fila -w igual a 0 0 1), que es cuando concluiría la primera fase y empezaríamos la fase 2.
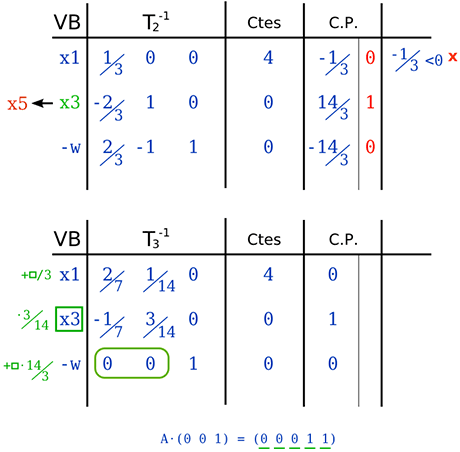
Fase 2
La nueva tabla T4-1 de la fase 2 será exactamente igual con respecto a las variables que están en la base, la base inversa (B-1), y la columna (0 0 1), pero es importante darse cuenta que volvemos al problema de máximos original, con su función objetivo original y a utilizar la matriz B en lugar de la Matriz A.
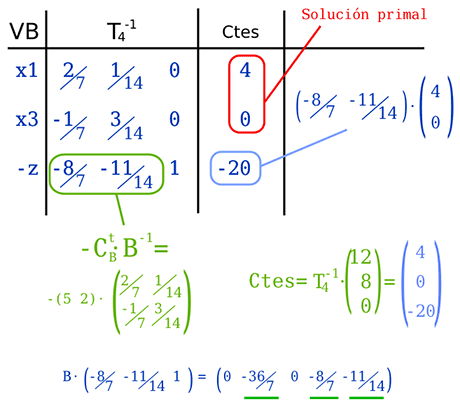
La última fila, pasa a convertirse de -w (fase 1) a -z (fase 2) y se pasa a calcular las siguientes zonas:
- -CBt · B-1: Los valores siguientes (en verde) se calculan nuevamente, aplicando esta fórmula con los nuevos valores, donde CBt es ahora X1 y X3 en la función objetivo original y B-1, que también ha cambiado.
- Ctes: Hay que actualizar los beneficios realizando la multiplicación de la tabla actual (T4-1) por las constantes del problema original, o sea la columna (12 8 0). Se puede ver también, que el valor objetivo se puede calcular de la forma indicada en azul.
Ahora solo tenemos que volver al paso del cálculo de los costos relativos (¡Ojo! Ahora con la matriz B), y seguir iterando hasta llegar al final.
En nuestro caso, hemos llegado al final porque todos los costos relativos son menores o iguales a cero (problema de máximos) y por lo tanto, se trata de una solución óptima no única para nuestro problema:
- X1: 4 (está en la base)
- X2: 0
- X3: 0 (está en la base)
- X4: 0
- X5: 0
Al llegar a una solución óptima, debemos saber que si una de las variables básicas es 0, entonces el problema tiene más de una solución.
Se puede utilizar el siguiente Applet Java (de Timothy J. Wisniewski) para comprobar problemas con el algoritmo Simplex Revisado: