¡Ojo! Hago directos en Twitch sobre desarrollo web, ¿Te apuntas? ManzDev
Teoría de la evidencia de Dempster-Shafer
Escrito por J. Román Hernández Martín
¡OJO! Si no eres informático o estudiante de ingenieria computacional, probablemente este artículo no te interese.
A continuación voy a explicar la resolución de un problema de Representación del conocimiento, de la materia Inteligencia Artificial, más concretamente basado en la teoría de la evidencia de Dempster-Shafer. Espero que a los alumnos que cursen dicha asignatura les sirva de apoyo.
En el hipotético ejercicio que vamos a exponer, se plantea que en un conjunto universo de hipótesis D, tenemos la opinión de tres expertos informáticos ante un problema desconocido en un ordenador.

- El primer experto es un brillante gurú informático, conocedor del mundo del software libre y los detalles más escondidos del software. Opina que los problemas del sistema estan causados por Virus, un disco duro dañado o conflictos de hardware con una medida de certeza de 0,6.
- El segundo experto es un reconocido especialista, certificado en Microsoft y con un amplio conocimiento en el sector. Opina con una medida de certeza de 0,7 que el problema está debido a un disco duro dañado, conflicto de hardware, incoherencias del registro o una tabla de particiones incorrecta.
- El tercer experto es un usuario común, pero con una lógica muy acertada y experiencia ante anteriores problemas similares. Este experto desconfirma la hipótesis de que sea cosa de Virus, disco duro dañado, conflicto de hardware, incoherencias del registro o tabla de particiones incorrecta. Su medida de certeza es de un 0,8.
El problema nos pide, teniendo en cuenta el orden de los expertos:
- La asignación de medidas de prob. de m1 (x) m2.
- La asignación de medidas de prob. de m1 (x) m3.
- La asignación de medidas de prob. de m1 (x) m2 (x) m3.
- La credibilidad de m1 (x) m2 para el conjunto de hipótesis disco duro dañado, conflicto de hardware e incoherencias de registro.
- La plausibilidad de m1 (x) m2 para el universo.
Lo primero, utilizaremos la teoría de conjuntos para abreviar y representar de forma más abstracta las entidades, así por ejemplo, cuando hablamos de un conjunto de decisión e1 = {A, B, C} nos referimos a un conjunto de decisión del primer experto que contiene los elementos Virus (A), disco duro dañado (B) e incoherencias de registro (C).
Así pues, los datos iniciales deducibles serían los siguientes:
- D = {A, B, C, D, E, F, G, H} = conjunto universal
- e1 = confirma {A, B, C} -> 0,6
- e2 = confirma {B, C, D, E} -> 0,7
- e3 = desconfirma {A, B, C, D, E} -> 0,8 => confirma {F, G, H}
Notar que el tercer experto desconfirma la hipótesis planteada, por lo tanto hay que realizar la operación D - e3. En todo caso, siempre hay que tener clara la siguiente leyenda:
- A = Virus
- B = Disco duro dañado
- C = Conflicto de hardware
- D = Incoherencias del registro
- E = Tabla de particiones incorrecta
- F = Spyware o Malware
- G = Incompatibilidad del sistema
- H = Problema de temperatura
Primer ejercicio
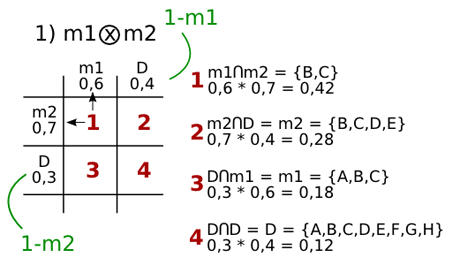
Dibujar una rejilla donde se colocaran por filas y columnas las medidas de probabilidad (m1 para e1, m2 para e2, etc..). Resaltar que la probabilidad de D para cada caso, es el complementario del resto. Sin embargo, este tipo de ejercicio puede variar, si en alguna de las casillas nos da como resultado vacío, ya que habría que reducir el resultado de las demás casillas. Veamos el ejercicio 2.
Segundo ejercicio
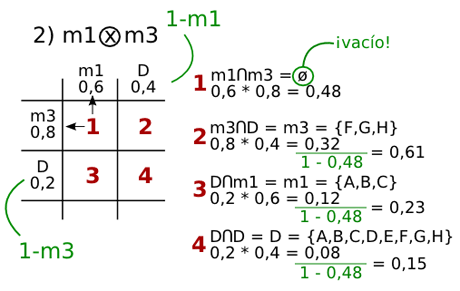
En este caso, vemos que al darnos como resultado un conjunto vacío, debemos restar el complementario de la probabilidad en las casillas restantes.
Tercer ejercicio
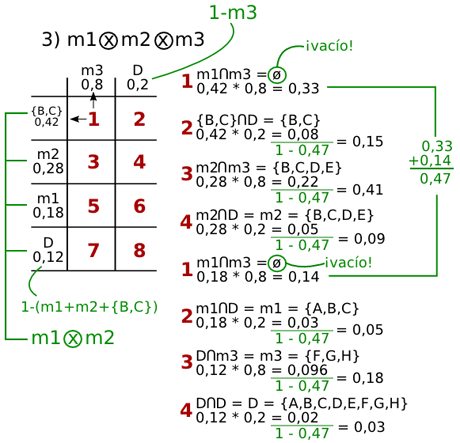
En este tercer caso, la asignación de medidas de probabilidad es más compleja, así que el proceso también lo será. Aprovecharemos que ya hemos realizado la operación m1 (x) m2 (Apartado 1), para utilizar los grupos de las casillas resultantes y utilizarlas para crear la nueva rejilla, que ahora tendrá dimensiones mayores.
En este caso, además, hay dos intersecciones que dan como resultado vacío, por lo tanto, habrá que sumarlas para restarlas como hicimos en el apartado anterior.
Yushs nos avisa de que hay una errata en el punto 3 de este apartado. En los comentarios lo menciono más detalladamente. Si puedo, desde que tenga algo de tiempo intentaré corregirlo.
Cuarto y quinto ejercicio
En estos últimos ejercicios, se nos plantea el problema de averiguar la la credibilidad y plausibilidad de m1 (x) m2. Como esta operación la hemos hecho previamente, las casillas resultantes {B,C}, m2, m1 y D deben comprobarse con el conjunto dado en el ejercicio, en este caso {B,C,D}.

Para averiguar la credibilidad, debemos asegurarnos de que se incluyan todos los elementos en cada uno.
Por otra parte, para averiguar la plausibilidad, debemos comprobar que se incluye al menos uno de los elementos especificados.
Eso es todo. Espero no haberme equivocado en la transcripción del problema y que a los alumnos que cursen la asignatura les sirva de ayuda.
